The following applications of supply and demand relentlessly use the idea that markets clear. Price adjusts to equate quantity supplied and quantity demanded. Competition is drives this adjustment. When there is excess demand, buyers compete with each other to access to scarce goods. When there is excess supply, sellers compete with each other to get access to scarce buyers.
The analysis of the previous section looks at supply and demand for a particular quality. So competition takes place on the single dimension of the monetary price. But as we will see below, when price is constrained by legislation that mandates a ceiling or a floor, other mechanisms beyond the monetary price are used to clear the market. So while we maintain the result that price adjusts to clear the market, we will eventually broaden our concept of price to go beyond the money price to include time or even quality changes
This is all just another way of saying that there are no shortages or surpluses. They are eliminated by prices adjusting. This is a highly simplified view of the world, but as we will see it leads to a number of useful results that capture the essence of how markets respond to various forms of government intervention. I want to thank Deirdre McCloskey who in Econ 300 at the University of Chicago showed us the power of supply and demand and provided much of the framework I present here.
Taxes
Let’s analyze a tax on gasoline of 10¢ per gallon. Assume that this is the only tax on gasoline. Assume that in the absence of the tax, quantity supplied (Qs) equals quantity demanded (Qd) at 75¢. (This is an old example, but to keep from redrawing the graphs, I’ll keep the numbers unchanged.) What will be the effect of the tax? The first problem is to figure out the new equilibrium. Your first thought should be to ask who the tax is imposed on, sellers or buyers.
A 10¢ per gallon tax on buyers requires buyers to keep track of their purchases and send 10¢ to the government for every gallon they buy. A 10¢ tax on sellers requires sellers to keep track of how many gallons they sell and send the government 10¢ for each gallon they sell. It seems obvious that buyers prefer the tax to be imposed on sellers and that sellers prefer the tax to be imposed on buyers. In fact, it doesn’t matter who the tax is imposed on, as long as people obey the law and pay the tax as required. We will assume for now that nobody cheats on their taxes. We will relax this assumption later.
Suppose that buyers must send in the tax payments. If the legislation requires that buyers send in the tax payment, then the price that buyers must pay for a gallon of gas is no longer equal to the price at the pump. They must pay the price on the pump PLUS 10¢. Sellers will still receive the price on the pump. A tax on buyers means that buyers pay 10¢ more than sellers receive.
Suppose that sellers must send in the tax. If this is how the legislation is written, the price sellers receive is no longer equal to the price at the pump. The price received is the price on the pump MINUS 10¢. A tax on sellers means that sellers receive 10¢ less than buyers pay.
Whether the tax is on buyers or on sellers, buyers pay 10¢ more than sellers receive. This must be true in equilibrium, regardless of the price on the pump. Look at the pre-tax equilibrium: price equals 75¢. What is the new equilibrium price? This question doesn’t make sense any more. (Why not?) There are now two equilibrium prices, the price that buyers pay in equilibrium, and the price sellers receive. We know that there is a 10¢ difference between them. The new equilibrium is going to have an equilibrium price that buyers pay, and an equilibrium price that sellers receive, such that Qs = Qd.
Where are such prices? Let’s guess. It’s OK to guess as long as we have a rule to determine whether or not the guess is good. A good guess is a guess where Qs = Qd. Every other guess is bad. Here’s a guess: the equilibrium price that sellers receive stays the same at 75¢ while the price buyers pay goes up to 85¢. Sellers “pass on” all of the tax. Since sellers are sending the tax money on to the government, we can think of two ways that the tax affects real world gasoline prices. Either the seller posts a price of 85¢ and says that it includes the tax, or he posts a price of 75¢ and tacks on the ten cents when you pay. The former way is the way real world gas stations handle the gasoline tax. The latter way is the way most stores handle sales tax. In either case, the seller gets 75¢ for each gallon sold because he must send in the 10¢ to the government. The buyer pays 85¢ for each gallon.
Can this be an equilibrium? Does Qs = Qd when buyers pay 85¢ and sellers receive 75¢? Nope. Look at figure 1. What is the Qs when suppliers receive 75¢? Q*. What is the Qd when buyers pay 85¢. Q’, which is less than Q*. There is excess supply. The price sellers receive must fall. How far will it fall? Let’s make another guess. Suppose the price falls to 65¢ on the pump so that buyers pay 75¢. Can this be an equilibrium? Nope. Now there will be excess demand. (Prove this to yourself. Use the logic we used to rule out the equilibrium where sellers received 75¢ and demanders paid 85¢.) Excess demand will drive up the price buyers pay and sellers receive.
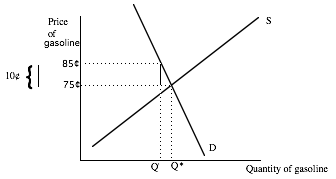
Figure 1–Making the wrong guess about the new equilibrium with a 10¢ tax
So the equilibrium price that buyers pay is between 85 and 75. The equilibrium price sellers receive is between 75 and 65. Not very exact. The exact answer is that the new equilibrium QUANTITY will be where there is a 10¢ vertical distance between the supply and demand curves. This is shown as the quantity Q0 in figure 2. Given the particular shape of the supply and demand curves in figure 2, buyers pay 82¢ and sellers receive 72¢. When buyers pay 82¢ and sellers receive 72¢, quantity supplied equals quantity demanded.

Figure 2–Equilibrium when there is a 10¢ tax on gasoline
The general rule for finding the new equilibrium under a tax, is to find the place in the supply and demand curve diagram where there is a vertical wedge equal to the size of the tax between the supply and demand curves. Think of a toothpick that has a height of 10¢. It is shown in the figures as the bracketed distance. Keep the toothpick perfectly upright and slide it into the gap between the supply and demand curve to the left of Q*. When it just touches both the supply and demand curve, you have found the new equilibrium quantity. At that quantity, the height of the supply curve is the new equilibrium price sellers receive, and the height of the demand curve is the new equilibrium price that buyers pay.
What is the effect of tax? A tax raises the price buyers pay and lowers the price sellers receive. If the seller physically sends in the money for the tax, then the price on the pump will be 82¢ (or it will be 72¢ and the 10¢ is tacked on at the register) which will be the price buyers pay, and sellers will get to keep a net of 72¢. If the buyers send in the tax, the price on the pump will be 72¢ and buyers will still pay 82¢. It doesn’t matter whether the buyer pays the tax or the seller pays the tax in the physical sense of who sends in the money. The price buyers pay and the price sellers receive is determined by competition through the shapes of the supply and demand curves. The price on the pump is free to adjust.
It is easy to get confused by real world gasoline stations where the price says 82¢ with a note that this includes a 10¢ state gasoline tax. This might make you think that the tax is always tacked on to the price at the pump and that a 15¢ tax would lead to a price of 87¢. It is true that the tax is always higher than the price on the pump in the real world by the amount of the tax. Just don’t forget that the price on the pump CAN CHANGE and is affected by excess supply and demand.
A tax reduces the quantity bought and sold. It is useful to think about the intuition of why the number of transactions go down. Before the tax, a buyer bought a gallon of gasoline as long as value was greater than the price. Sellers were willing to sell a gallon of gasoline as long as the price exceeded the cost. Because of competition and the law of one price, this meant that buyers and sellers exchanged money for a gallon of gasoline whenever the value of the gallon to the buyer exceeded the cost of the gallon to the seller.
Under a tax, there is a new set of rules. Now when buyers and sellers exchange money for gasoline, think of a government agent standing there collecting the 10¢ from one of them.
Now, if the buyer values the gallon by a nickel more than it costs the seller, they won’t make the exchange. This exchange does produce a net benefit of the transaction of a nickel.
But because one of the parties to the transaction or the two of them combined must pay an additional 10¢, the net benefit from the transaction is now negative; it won’t be worth it anymore. Transactions that took place in the absence of the tax won’t take place anymore. Which transactions? Those transactions where the combined net benefit to buyer and seller is positive but less than 10¢. You can see those transactions in figure 2–the transactions between Q0 and Q*.
A tax also yields revenue. This revenue is a transfer from the producers and consumers of gasoline to the government. We assumed the government does something with this money—transferring it to farmers or aerospace firms or school lunch recipients.
If it doesn’t matter whether the tax is physically imposed on buyers and sellers, why are sales taxes such as those on general merchandise and those on gasoline always physically imposed on the seller and not the buyer? There are two possible answers. One is that politicians like to impose taxes on businesses because businesses don’t vote and people do.
This explanation assumes that people are stupid and believe that the physical imposition of the tax determines who really pays it.
There is a better explanation without assuming voter ignorance. It is costly to enforce the tax collection. It is cheaper for the government to enforce collection by firms than it is collection by consumers. This is the beginning of the answer. Can you think of why it might be cheaper to enforce payments by firms rather than consumers? One answer is fairly obvious–there are many fewer sellers of gasoline than there are buyers. It is easier to keep track of them and to check up on them.
The second reason is more interesting. It is cheaper to monitor firms rather than consumers because firms keep track of their receipts through register tapes while consumers throw their receipts away. The real question is then why do firms keep their register tapes? They would prefer to evade the tax–collect it from the consumer in the form of the higher price and then not send in the money to the government. The register tape provides a record of a firm’s sales which allows the government to see whether they are paying their share of the tax. A firm can evade the tax by not ringing up all receipts. Taxi drivers do this all the time. They don’t turn on the meter and avoid a record of the fare being collected. This allows taxi drivers to avoid income tax and sometimes avoid paying the company renting them the cab.
The firm rings up transactions on the register even though this keeps them from cheating on the sales tax. Why? Perhaps they are civic minded. Perhaps. But surely there is a distribution of civic-mindedness, some are a lot more civic-minded than others. Wouldn’t some firms avoid using registers so as to be able to cheat on their taxes? Surely some do.
But maybe there’s another benefit from keeping register tapes, or a cost avoided. The benefit of ringing up transactions is that it keeps employees from stealing from the firm.
Imagine a firm without a cash register. The owners then have to trust that their employees will always turn over the right amount of money at the end of the day. The cash register provides a record of receipts to prevent employees from cheating. Evidently, the gains from monitoring employees via the register receipts combined with a desire to be a good citizen outweighs the potential gains from tax evasion for most firms.
This motive for the cash register explains other phenomena. At some stores your purchases are free if your cashier does not give you a receipt. This gives customers the incentive to monitor the employees’ honesty. For years the post office didn’t have cash registers. There was a cash drawer, but the purchases were not rung up. How did the post office maintain employee honesty? At the beginning of each day, each salesperson was given a stock of stamps and envelopes. The employee had to account for these at the end of the day or provide the money.
While this system does reduce the ability of post office employees to sell to the public and pocket the proceeds, it had two unfortunate consequences. The first was that the employees did all their calculations by hand on little scraps of paper. The second was far worse. You waited in line for 20 minutes. When you got to a salesperson, they informed you that they were out of long envelopes, but they had short ones. I could never understand how one person could be out of something. Couldn’t they just get some from their fellow employee, two feet away? But they couldn’t, unless they bought them from them. This problem seems to be resolved; most post offices now have cash registers.
Now let’s see if you understand how a tax affects equilibrium. Think about the equilibrium when the tax is in percentage terms, rather than in cents. For example, consider a 10% tax on gasoline. To get you started, here are some hints. Assume that the price on the pump does not include the tax. So a pump price of 70¢ means that buyer or seller must send the government 7¢. A price of 80¢ means that buyer or seller must send the government 8¢ etc. Here is a hint: a 10% tax means that buyer always pays 10% more than the seller receives. Can you figure out where the new equilibrium will be?
Here is how you can know whether you understand taxes. Suppose the original price of gasoline is $1.00 per gallon. A 10¢ tax and a 10% tax will not have the same effect. It seems obvious that they would both increase the price of gasoline by 10¢, but they do not since the price at the pump will not stay at $1.00. Can you prove why the two taxes must be different and which one will raise more money for the government?
Other questions to ask: How do consumers in two different markets feel about a tax of 50¢ per unit if each market has the same supply curve, but in one market the demand curve is more elastic? Which market raises more revenue?
Subsidies
A subsidy is the opposite of a tax–it is a promise by the government to send a buyer or seller a payment for making a transaction. For every foot of insulation you put in your attic, the government will send you $1. Or for every medical procedure done on an old person, the government pays 50% to the doctor. Consider the subsidy to insulation. A subsidy of $1 introduces a $1 divergence between the price sellers receive and the price buyers pay. In this case, however, the price sellers receive exceeds the price buyers pay by $1. Can you find a quantity of insulation in a supply and demand diagram where the price sellers receive exceeds the price buyers pay by $1? What has happened to quantity relative to Q*? How much revenue does the government have to raise to finance the subsidy payments?
Price Controls
Here is a more complicated interference with the market. There are two types of price controls–a maximum price called a price ceiling and a minimum price called a price floor. Let’s consider a price ceiling on gasoline, a situation which existed at various times in the 1970s.
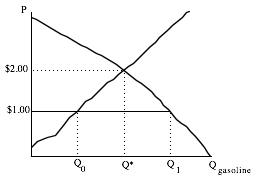
In the above figure, the market price in the absence of government intervention would be $2.00. The government decides this price is too high. They pass a law decreeing that no producer can sell gasoline to the public for more than $1.00. (Here as always, we assume that producers and retailers are the same entity.) Assume that this law is enforced under the threat of boiling in a vat of hot oil for a very long time. Or make any other assumption you wish to insure that the law is obeyed. You may wish to consider whether people have an incentive to obey the law without this threat, and how the analysis would change if enforcement were imperfect.
What is the new equilibrium? Remember the definition of an equilibrium–quantity supplied must equal quantity demanded. This occurs at P* of $2.00, but price cannot be $2.00 because we have assumed that the law is perfectly enforced. To find the equilibrium we must find a price or prices equal to or less than $1.00 where Qs equals Qd. Let’s start on the side of the suppliers. What price will suppliers receive in equilibrium? It can’t be greater than $1.00 because the law rules it out. Can it be less than $1.00? At prices less than $1.00, there is excess demand which puts upward pressure on price. This upward pressure on price pushes price up to $1.00 where it can go no further. If price cannot exceed $1.00 and cannot be less than $1.00, then the price suppliers receive must be exactly $1.00. At $1.00 there is still excess demand, but there is no force that can change price from $1.00 for suppliers. So suppliers receive $1.00 and produce Q0.
Are we done? We have found the price suppliers must receive, and the quantity they will produce when receiving that price. But quantity supplied does not equal quantity demanded. So we have not found an equilibrium. Something must eliminate the excess demand at $1.00. In an unconstrained market, price would rise to eliminate the excess demand. The increase in price would increase the quantity supplied and decrease the quantity demanded until the two were equal at a price of $2.00. But this cannot happen. What will happen?
The price demanders pay must go up until Qd equals Qs. This only occurs when consumers pay Pa per gallon, shown below:
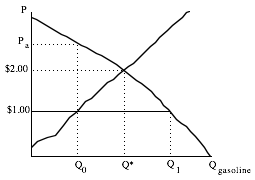
At price Pa per gallon, quantity demanded falls to Q0 which equals quantity supplied, the quantity supplied at $1.00. Price MUST rise to Pa for consumers. This is the only price that consumers can pay where quantity demanded is equal to quantity supplied. We have already proven that quantity supplied must be Q0, because suppliers must receive $1.00. So we have found an equilibrium, but it is not very satisfying. How can consumers pay Pa per gallon when suppliers receive only $1.00? What competitive force insures that price must rise to Pa?
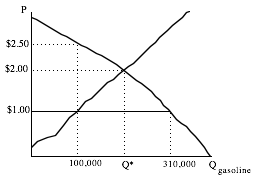
Let’s see how the market will work with the price ceiling. The figure below shows the market with some numerical values filled in to aid the discussion:
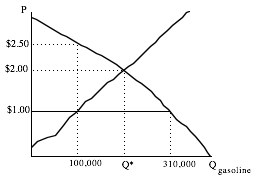
The quantity demanded when price equals $1.00 per gallon for the particular demand curve shown is 310,000 gallons. Assume that each car holds 10 gallons and that everyone fills up. So if price were $1.00 and people could fill up their cars at that price, 31,000 customers would show up per day at gas stations to buy gas. But there is only enough gas to fill up 10,000 cars. What is going to happen? If all 31,000 people show up on the first day, 21,000 will ultimately be disappointed. Some of them will go home immediately as soon as they see the crowds at gas stations. Others will wait. At the end of the day, some people will decide that the waiting time raised the price of gasoline sufficiently so that they will decide to drive less frequently, and fill up less often.
On the second day of price controls, there are again 31,000 people who would LIKE to fill up their cars at the price of $1.00 per gallon. But having heard or seen that the station closed on the previous day after serving only 10,000 customers, these 31,000 potential customers realize that even though they would all like to buy gas at $1.00, they all will not be able to. To make sure you are one of the 10,000 customers who gets to purchase gas, you must get in line before the station opens. But now the price of gas is no longer $1.00. It is $1.00 plus the value of the time spent waiting.
How early will people have to get up to buy gasoline? We can get an easy answer by making an “unrealistic” assumption about how people can fill up their cars. Suppose people can fill up their cars with gasoline by driving next to the pump and saying the magic word “Petroleum!,” so that it essentially takes zero time to physically fill your tank.
Suppose gas stations open at 9:00. Suppose there are 200 identical gas stations in the market for gasoline. Evidently, each station wants to supply 500 gallons when the price is $1.00. Because each customer buys ten gallons each time, each station can serve 50 cars a day. Under these assumptions, each station will have 50 cars in line before 9:00. How much before 9:00? Suppose all people value their time at $10 per hour. Then all cars would get in line at 7:30. Where did 7:30 come from? IF you had to get in line at 7:30, you will have to spend 1.5 hours waiting to have your tank filled. The value of that time is $15, or $1.50 for every gallon you buy. So the actual price of gasoline, Pa, inclusive of time, is going to be $2.50.
A person who gets in line at 8:00 will find that the station has run out of gas before he arrives. Suppose he didn’t. Suppose he found out that he could get in line at 8:00 and there was still gas available at 9:00 to serve him when the station opened. Then the value of time lost would be $10, and the price per gallon would be $2.00. But when the price is $2, more people want to get in the line than there is gas available. Some of them will be disappointed and will not get gas. They will realize they will have to get to the station earlier in order to be one of the cars getting gas.
Why will exactly 50 cars get in line? More than 50 might get in line, but some of them will not get gas–the station closes before they can get served. Eventually people will start to figure out how many cars get served and will not get in line if they don’t think they’ll get gas.
If cars cannot fill up instantaneously by saying a magic word, the dynamics of the line are different. Suppose it takes 6 minutes to fill up a car and each gas station has 1 pump, and there are again 200 identical stations. Each customer takes 6 minutes, so each station is open for 300 minutes (50 customers, each taking 6 minutes) or five hours. Each station announces it will open at 9:00 and close at 2:00. How will the line work? One car will get in line at 7:36, another at 7:42, another at 7:48, and so on. At 9:00, when the station opens, there will be 15 cars in line. The car that got in line first at 7:36 will start filling at 9:00 and be finished at 9:06 having spent 90 minutes in line. These 15 cars will proceed through the station, each filling up and each having waited 90 minutes or $15 worth of time. The remaining 35 cars get in line one by one every 6 minutes. At 12:30, the 50th car gets in line behind 14 others. No one gets in line after 12:30 because the station closes at 2:00 and it will have exhausted its supply then. These last 15 cars take 90 minutes to fill up. If you drive by the station anytime between 9:00 am and 12:30 you will see 15 cars in line and you will figure on an approximate wait of 90 minutes. Can you figure how market forces will make sure that cars arrive approximately every 6 minutes? How does this get coordinated in the real world?
(All of our gasoline stories assume we have ignored the fact that even without price controls it takes 6 minutes to pump gas. If we wanted to take this into account, would we have to change P* in the equilibrium without price controls? Would it change the story in this paragraph? ANSWER: In the equilibrium without price controls, we assume people’s demand curves take into account the fact that it takes time to fill up your car. So there is no change in P*. In the paragraph above, the first car would actually get in line at 7:30, finish at 9:06 for a 96 minute experience, an additional 90 minutes of waiting time, which is exactly what it takes to clear the market.)
You can continue to make the analysis more complicated by allowing for people having different values of time, stations having different amounts of gasoline and different numbers of pumps, people don’t always fill up and so on. But the fundamental result is unchanged–as long as gasoline is sold at a price below P*, some mechanism will evolve to make sure that the full price is above the market price. In the case we have just discussed, TIME is used to allocate scarce gasoline.
Under price controls, time, rather than money is used to allocate the scarce gallons. Consumers compete for them by waiting. The value of the time spent in line is equal to the cross-hatched box in the diagram below:
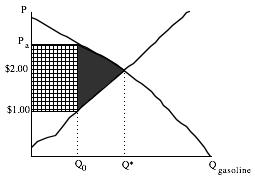
The height of the box is the value of the time per gallon. The width is the number of gallons waited for. The area then, is the total value of time spent waiting for gasoline. Without price controls, this time would be available for people to enjoy. The enjoyment people received from this time is gone now. In our example, Pa was equal to $2.50, so the monetary value of the wasted time is $15 per tankful.
To see the waste from having people wait in line, think of an alternative method of allocating the Q0 gallons. For every tankful of gas, consumers must pay suppliers $10 in money and set fire to a shirt they have just purchased for $15. The waste is clear in this case–society has fewer shirts to enjoy. But what is weird about this story is who loses the value of the shirts. Think of a third alternative–for every tankful of gas you purchase you must give the seller $25, but sellers are forbidden by law to expand total production in the aggregate past Q0. In all three stories, consumers must sacrifice $25 to get a tank of gas. In one case they pay it all in cash. In the others they pay a mixture of cash and “something else” where the value to them of the something else is $15. The difference is that when money is used, the money is a transfer from consumers and suppliers. No resources are consumed.
In the other two methods, the time and the shirt method, real resources are paid and no one gets them. Using time rather than money throws away resources rather than transferring them into the hands of suppliers.
Incredibly, the waste from price controls is not reduced by consumers finding something useful to do in their cars as they wait. This is one of the great unintuitive results of economics. Can you see why it’s true?
Here is a summary of the gasoline price control example:
- Assume that each car holds 10 gallons and that everyone fills up.
- So if price were $1.00 and people could fill up their cars at that price, 31,000 customers would show up per day at gas stations to buy gas.
- On the second day of price controls, there are again 31,000 people who would LIKE to fill up their cars at the price of $1.00 per gallon. But having heard or seen that the station closed on the previous day after serving only 10,000 customers, these 31,000 potential customers realize that even though they would all like to buy gas at $1.00, they all will not be able to.
- To make sure you are one of the 10,000 customers who gets to purchase gas, you must get in line before the station opens. But now the price of gas is no longer $1.00. It is $1.00 plus the value of the time spent waiting.
- How early will people have to get up to buy gasoline? We can get an easy answer by making an “unrealistic” assumption about how people can fill up their cars. Suppose people can fill up their cars with gasoline by driving next to the pump and saying the magic word “Petroleum!,” so that it essentially takes zero time to physically fill your tank.
- Suppose there are 200 identical gas stations in the market for gasoline.
- Suppose gas stations open at 9:00. Evidently, each station wants to supply 500 gallons when the price is $1.00. Because each customer buys ten gallons each time, each station can serve 50 cars a day. Under these assumptions, each station will have 50 cars in line before 9:00. How much before 9:00?
- Suppose all people value their time at $10 per hour.
- Then all cars would get in line at 7:30. WHAT? Where did 7:30 come from? IF you had to get in line at 7:30, you will have to spend 1.5 hours waiting to have your tank filled. The value of that time is $15, or $1.50 for every gallon you buy. So the actual price of gasoline, Pa, inclusive of time, is going to be $2.50.
- If cars cannot fill up instantaneously by saying a magic word, the dynamics of the line are different. Suppose it takes 6 minutes to fill up a car and each gas station has 1 pump, and there are again 200 identical stations. Each customer takes 6 minutes, so each station is open for 300 minutes (50 customers, each taking 6 minutes) or five hours. Each station announces it will open at 9:00 and close at 2:00. How will the line work? One car will get in line at 7:36, another at 7:42, another at 7:48, and so on. At 9:00, when the station opens, there will be 15 cars in line. The car that got in line first at 7:36 will start filling at 9:00 and be finished at 9:06 having spent 90 minutes in line. These 15 cars will proceed through the station, each filling up and each having waited 90 minutes or $15 worth of time. The remaining 35 cars get in line one by one every 6 minutes. At 12:30, the 50th car gets in line behind 14 others. No one gets in line after 12:30 because the station closes at 2:00 and it will have exhausted its supply then. These last 15 cars take 90 minutes to fill up. If you drive by the station anytime between 9:00 am and 12:30 you will see 15 cars in line and you will figure on an approximate wait of 90 minutes. Can you figure how market forces will make sure that cars arrive approximately every 6 minutes? How does this get coordinated in the real world?
Some further thoughts on price controls
In the gasoline example, we have assumed that waiting rations gasoline. This is what happened in the 1970s when price controls were imposed. But waiting is only one way the market responds to price controls. The other important response to a price ceiling is the degrading of quality. By reducing quality, suppliers evade the price control. What is fascinating is that some and perhaps all consumers WANT quality degradation. How can that be? To see a crude example, if the market clearing price for gasoline is $2 and the government places a price ceiling of $1, a gas station that sells gallons of gasoline that are only 1/2 a gallon will have a lot of customers. The effective price will be $2 per actual gallon and customers there will be able to avoid the time costs.
This type of evasion is relatively easy to police, but other techniques may prove more difficult. The re-naming of a gallon example raises the question of why the government ever passes price control legislation. When all consumers are identical, all consumers are harmed by price controls. So a rational model of price controls must rely on differences among consumers that are exploited by legislators. Such a model would be useful in explaining the differences between a price control and a tax that achieve the same reduction in quantity.

