The firm’s goal is to maximize profits, π. In order to do this it must decide what quantity of a good to produce given costs, technology and demand. A competitive firm is assumed to be able to sell as much as it wants at the market price without affecting price. So it takes price as exogenous (beyond it’s control) and does not worry about demand. In addition, for our purpose we’ll assume the firm operates efficiently, that is, whatever the level of production that the firm chooses, that level of production will always be produced at the minimum possible cost.
Profit is defined by the difference between total revenue (TR) and total cost (TC). Both TC and TR are functions of quantity. TR is defined as: (price per unit of the good)*(quantity of the good sold). It is a linear function, TR=Pq, where P equals the price of the good, q the quantity sold. The slope of the TR line is P and the price is the amount the firm receives if it produces and sells one more unit of the good. Marginal revenue (MR) is the additional revenue the firm gets from selling one more unit, given a particular level of sales. Therefore, marginal revenue is equal to P. The slope of the TR line is P, equal to MR. Because the firm takes price as given, our TR line has a constant slope. Total cost, TC, on the other hand, is a more complicated function of quantity. It may vary at different rates with different quantities, as we shall soon see.
Marginal cost (MC) is the increase in cost from producing one more unit of the good given the amount you are already producing. The marginal cost to produce your first ton of steel, in a certain time period, is probably higher than the MC of the hundred and first ton in that same period. To produce the first ton you must build a plant, buy equipment, train labor and pay for all of the fixed costs associated with opening a steel plant. The hundred and first ton involves only the cost of the ore, the energy, the man hours and other inescapable product costs. These costs were also included in the cost of the first, and every, ton. It is important to note that your million and first ton of steel may cost considerably more to produce—at this point, your plant may be too crowded with raw materials or too many employees to be working efficiently. When the operation becomes that large, supervising gets a lot tougher and costly, and you may have to pay higher prices to draw labor and capital away from other industries.
Let’s consider an example of one firm producing steel. Assume the price of a ton of steel is $12. The graph shows TC and TR. Notice, TC increases at a decreasing rate at first but eventually increases at an increasing rate.
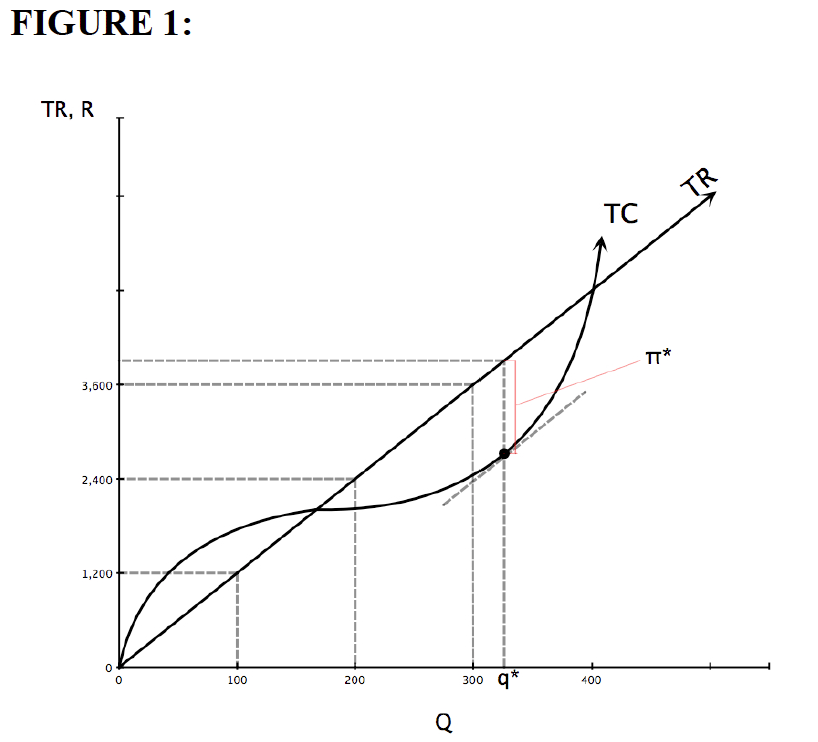
[Notice that even though TR is a 45° line, the slope is not 1 but 12—the units on the two axes are not the same]
The owner of the firm wants to maximize profits, π, by maximizing the vertical distance between TR and TC. Remember, TR – TC = π. Just by looking you can tell that the quantity would be somewhat over 300 tons. The way to tell exactly is to find the point on the TC curve which is tangent to a line with the same slope as that of the TR line. Here the slope of the TR line is equal to 12, the price of a ton of steel and the MR that ton will generate. At the point of tangency the slope of the TC curve equals the slope of TR curve. Since the slope of the TC curve at any point is the MC, we know that at the quantity of output corresponding to the point of tangency MC equals P (which we know also equals MR). By drawing a line parallel to TR and tangent to TC we can see that the profit maximizing quantity for the firm is about 325 tons. At this quantity, labeled q* on the graph, profits equal π*.
Since π* is the furthest possible distance between TR and TC a firm producing at the quantity q* will be maximizing its profit. Said another way, to find q* we find the point on the TC curve with the same slope as the TR curve, the quantity where MC = MR.
The quantity a firm produces is profit maximizing when MC = MR. This finding conforms to “the rule of the rational life” which says that you should keep doing something until its marginal cost is equal to its marginal benefit. As long as price is greater than marginal cost adding to production increases profits. When price is less than marginal cost, profits will go down if you increase production.
But, what does the firm do if the price changes?
Graphically, price is simply the slope of the TR curve. When the slope of the TR curve changes the tangency that determines q* will be at a different point on the TC curve:
FIGURE 2:
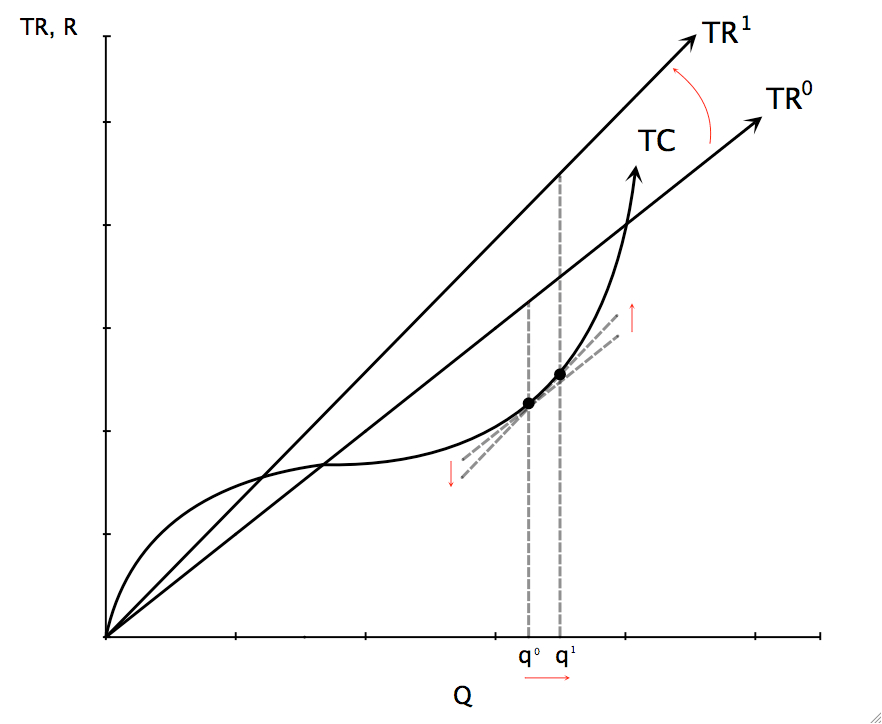
I’ve drawn TR1 steeper than TR0 indicating that price increased. The new tangency indicates a new profit maximizing quantity, q1, which is larger than q0. This should make intuitive sense. A firm should supply more to take advantage of the increased profit opportunity presented by a higher price. In this example we changed price and demonstrated that such a price change would result in a change in the optimum quantity. By repeatedly changing price and observing the various resulting quantities we could construct the supply curve for the firm. A supply curve is a simple, graphical representation of the profit maximizing level of output for the firm. We know that the supply curve is upward sloping because, as we raised price, optimum quantity rose also. We found the new quantity by setting price equal to MC. This implies that if we make a curve from our values of the slope of TC at different quantities, that MC curve would be our supply curve. By observing the changes in the slope of our simplistic TC curve we can construct the following graph of marginal cost (MC):
FIGURE 3:
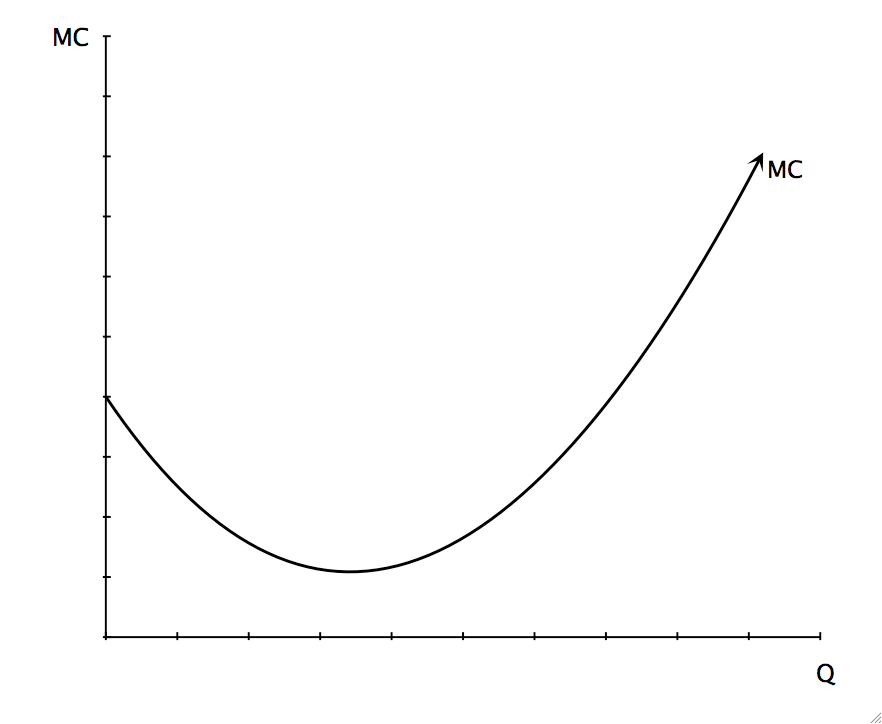
We assume throughout these problems that costs are being minimized–that there is no more efficient way to combine factors to decrease our costs of production. This is necessary to maximize profits, necessary but not sufficient.
How does a firm determine if it should produce?
A firm should produce only if it’s possible to earn a profit. By definition, this can occur only when TR > TC. Is there a quantity that “guarantees” the possibility of profit under the assumptions we’ve made? Yes, and considering average cost is useful in figuring out what that quantity is. Average cost equals TC/q. Average cost can be found using the TC picture by finding the slope of the line from the origin to the total cost curve for a particular quantity.
FIGURE 4:
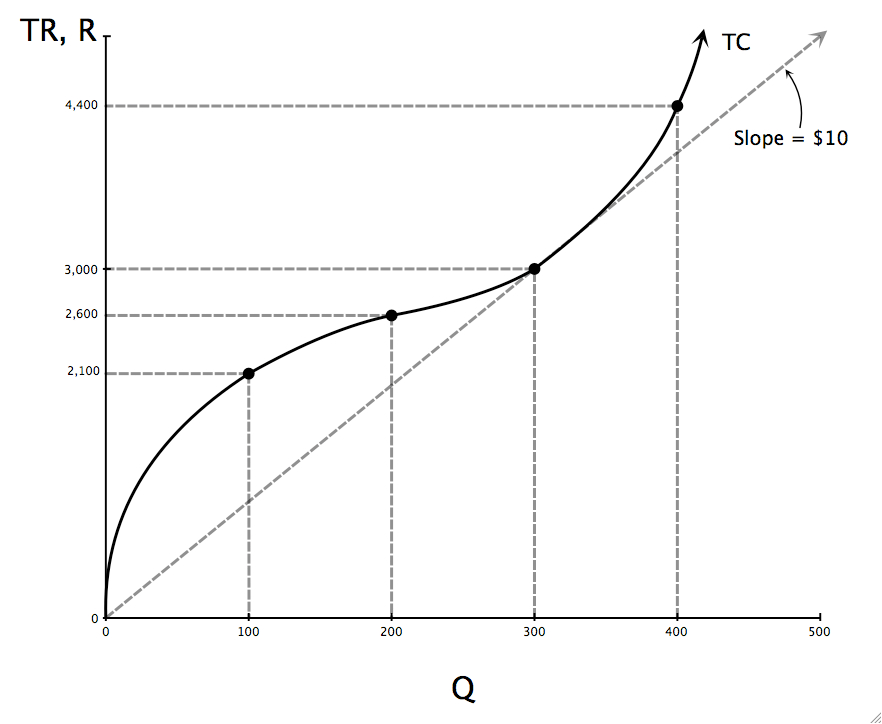
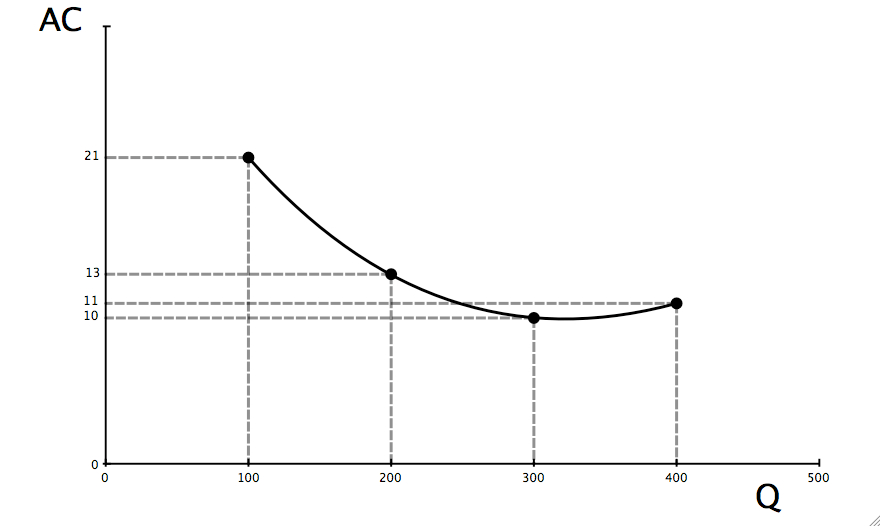
[Note the different scales on the Y-axis]
The above figure shows total cost and average cost using some numerical values. The key quantity is qe, the quantity where average cost is minimized. That quantity is 300 in this example. The value of average cost at this quantity is Pe. In the example above, it is $10. We give the value of average cost at qe the name pe because if price is below $10, there is no quantity the firm can choose that will produce positive profits. You can see this by imagining the TR line when p is less than $10–it will lie everywhere below the TC curve. Having TR < TC does not meet the goal of a profit maximizing firm.
When price equals Pe the firm produces where P = MC which means that the firm is making zero economic profits (even though they may still be registering revenues above recorded expenses and thus positive accounting profits). Since opportunity costs are not recorded expenses they aren’t considered in accounting profits, but must be included in the calculation of economic profit. If economic profit is zero then the firm is indifferent between continuing to produce and investing the money in the next best alternative.
If a hamburger stand can make more revenue with the same costs by selling chicken it should do so. Even if it is making positive accounting profits selling hamburgers its economic profits are negative, once the cost of the neglected opportunity to sell chicken is factored in. The stand’s opportunity costs are too high for it to maximize profit by remaining in the hamburger business.
Now we know enough to draw the firm(s) supply curve & the market supply curve…
A supply curve shows which quantities will be produced at different prices. Until price hits Pe the firm will not produce at all—the supply curve is a vertical line along the price axis. When price equals Pe the quantity produced equals qe. After qe, quantity produced is determined by the intersection of price and MC. The change in quantity with price is dependent on the MC curve, therefore, after qe, the supply curve is equal to the MC curve.
Let’s see what market equilibrium looks like. By bringing consumer demand into our picture we can determine how many firms will participate in this market. Suppose each firm in the industry has supply curve si:
FIGURE 5:
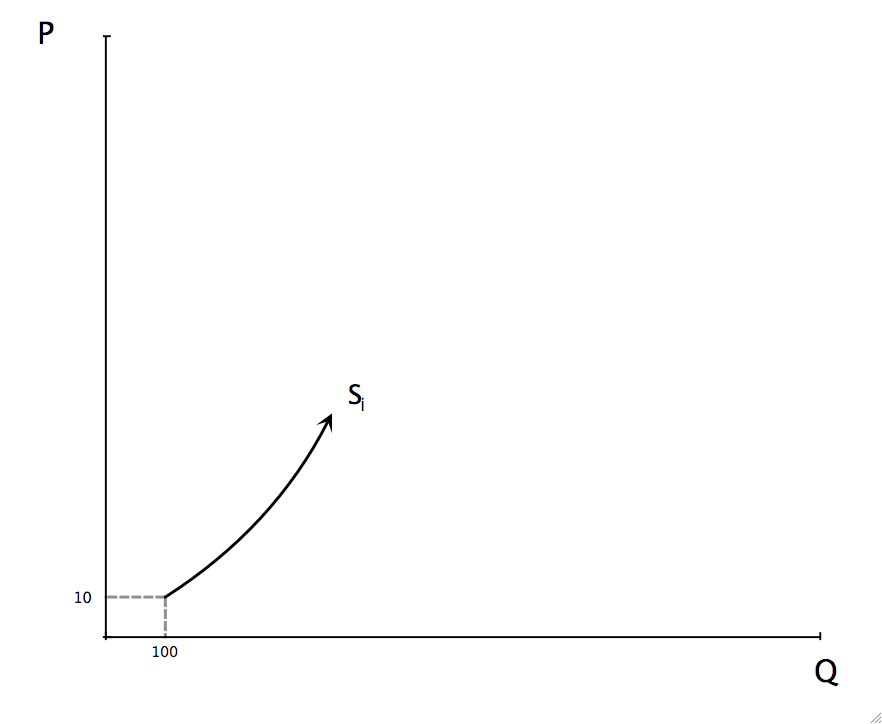
Suppose Qd at $10 is 900. Then Qs will equal Qd at P* = $10 and Q* = 900. Nine firms will be in the industry and each will be selling 100 units and make zero profits. Why? Well, suppose there were 10 firms in the industry. If all were to produce 100 units, then the supply curve would have to cross demand at a price below $10. If all the firms were to produce less than 100 units, all the firms would be losing money. The only option is for one firm to stop producing.
Supply and demand would then look like:
FIGURE 6:
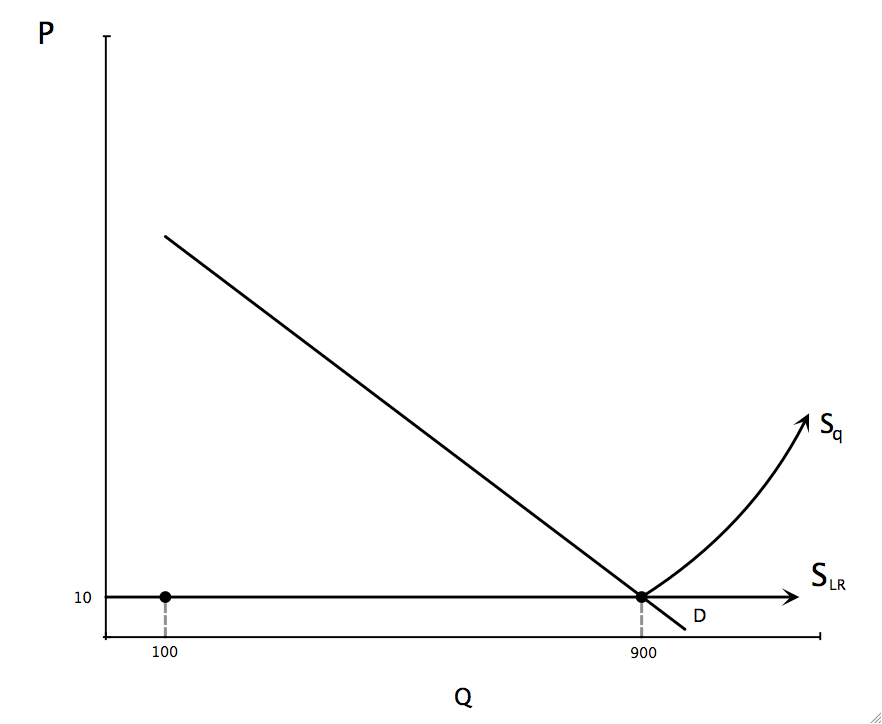
This situation is stable as long as nothing else changes. You should be able to explain why the situation is not stable when there are only eight firms in the industry (and why a ninth would enter) and understand why a tenth firm must go.
What if demand changes?
An outward shift in demand increases price in the short run, creating positive economic profits. These positive profits will last until the long run when new firms, attracted by positive profits, enter the industry, increase supply and thus decrease price until it once again equals Pe, or in the case here, $10. In the long run, in a perfectly competitive industry with identical firms, price equals Pe, Q* is determined by the quantity demanded at Pe, and the number of firms equals Q*/qe.
What if all firms aren’t identical?
A simple example of an industry whose firms may vary by entry prices would be one in which there is one firm or a finite number of firms with lower costs than the rest of the industry. In this kind of market you have two types of firms, the smart ones (say, IBM in the old days of the mainframe business or perhaps Apple in market for digital music players today) and the not-so-smart ones. The smart firm has a lower cost curve than the other firms; this may be because of patents or secret technology they control or maybe just a certain flair for business that allows them to produce the same product for less.
So there are a lot of firms with supply curve si but only one has figured out the technology that produces sj. I have assumed that each i type firm is again willing to enter when the price is $10, but a j type firm is willing to enter when the price is $5.
FIGURE 7:
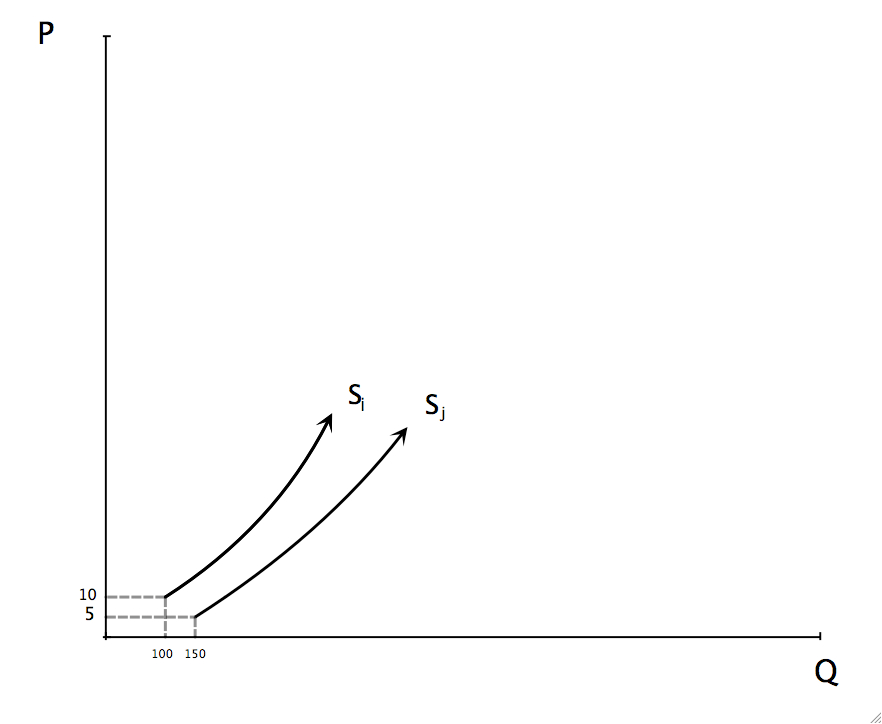
The market supply curve is then:
FIGURE 8:
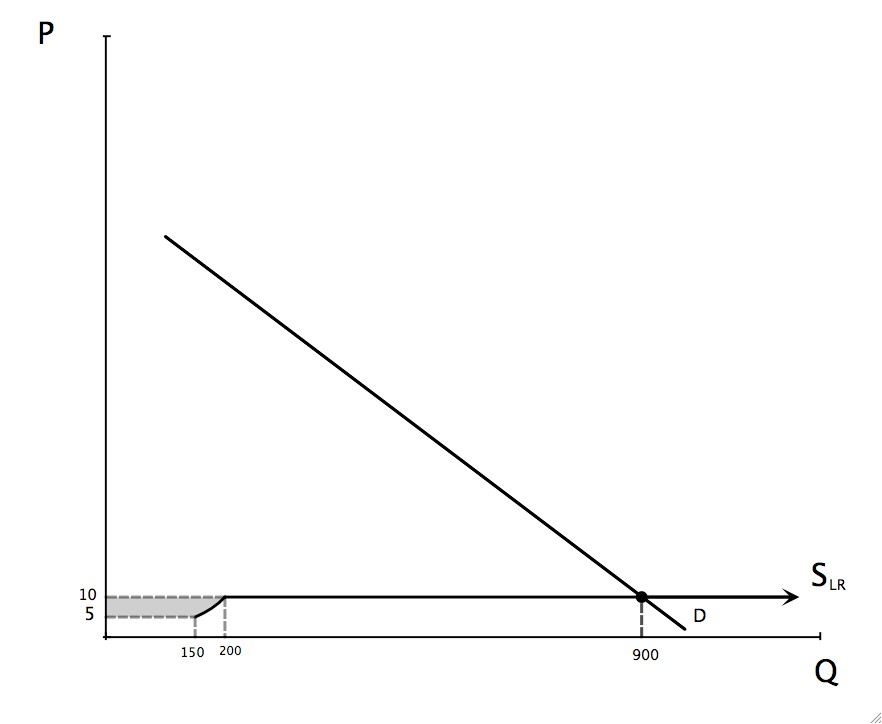
The dip is caused by the market supply curve following the individual supply curve of firm j. The equilibrium price and quantity are unchanged because the supply and demand curve still cross at the same point. As I have drawn it, the quantity supplied by firm j at P* is 200. One firm of the i type will be forced to leave the industry, leaving 7 i type firms with the j type firm in this industry. The shaded area represents the decrease in total cost (area under the market supply curve) to society of producing the product. All of this gain goes to the j firm which earns higher profits.
If all the firms figure out the j technology then the market supply curve becomes horizontal at $5. If we contrast the gain to society in the case where all firms are i firms to the case where all firms are j firms, the increase in net gain is the shaded area in Figure 9. In this case, this entire gain accrues to consumers. Producers make zero profits, consumers have benefited by the lower costs.
FIGURE 9:
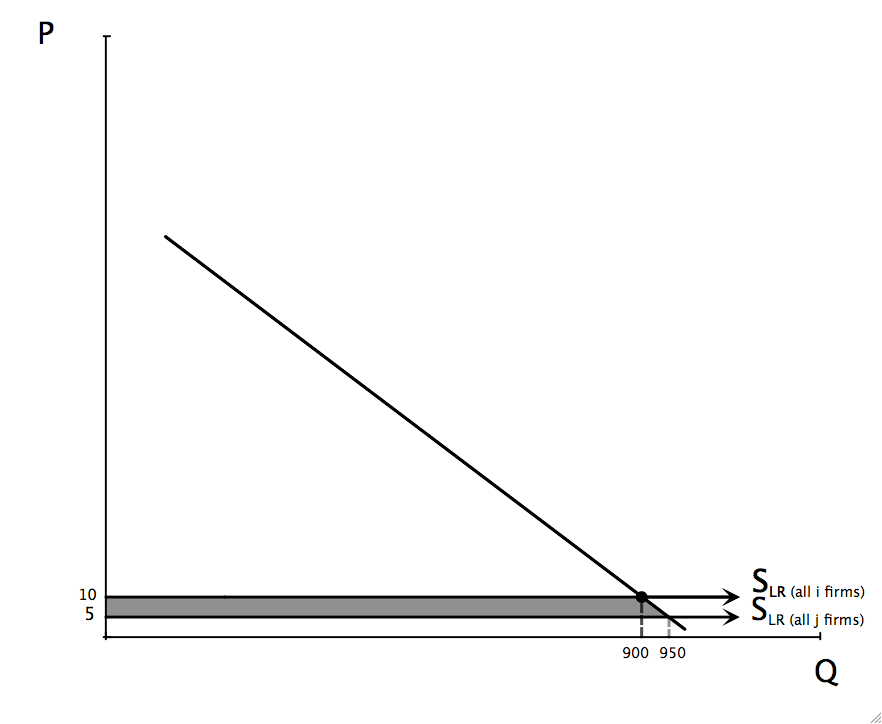
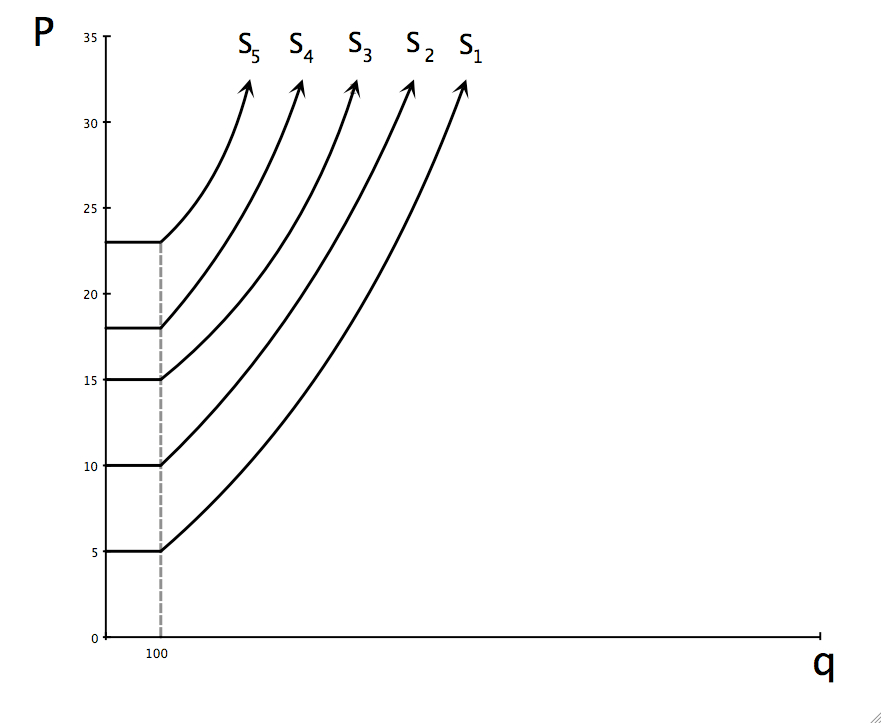
Finally we have the case where all firms are different. Suppose five firms know how to produce a good and they are the only five able to do it. All five have different entry prices but for simplicity, I will assume that all five have the same qe. This is shown below.
FIGURE 10:
What would the long-run supply curve look like?
FIGURE 11:
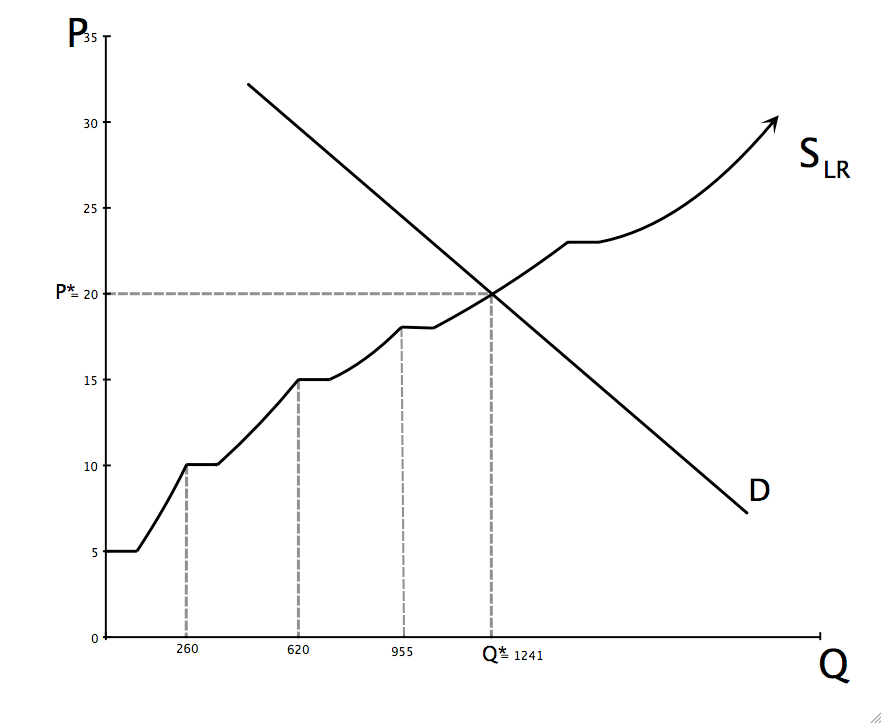
Equilibrium will again be determined by where S and D intersect. Given where the demand curve hits the supply curve there will be four firms in the industry and all of them will be making profits. The fifth firm can’t enter and compete for those profits because it will not be able to cover its costs. So profits can persist in the long run when firms cost advantages cannot be imitated. To make sure you understand the above picture, figure out what the firm with the supply curve s1 will do in equilibrium and what its profits will be (within a range). What is the total net gain to society in equilibrium?
A final example…
Here is an example to help you understand the theory of the firm. Suppose I am a firm that makes sweaters. I produce sweaters using knitting needles, yarn, and my time. If I don’t make sweaters, my next best alternative is working on a garbage truck which I can do for $3 an hour. It costs $1 to buy a pair of knitting needles (they last one day and then fall apart), and $1 for the yarn to make one sweater. The following chart describes the costs to me of knitting various numbers of sweaters.
| Numbers of sweaters/day | Total hours spent knitting | TC | AC | MC |
| 1 | 1 | $5.00 | $5.00 | $5.00 |
| 2 | 2 | 9.00 | 4.50 | 4.00 |
| 3 | 3 1/6 | 13.50 | 4.50 | 4.50 |
| 4 | 5 | 20.00 | 5.00 | 6.50 |
| 5 | 8 | 30.00 | 6.00 | 10.00 |
| 6 | 12 | 43.00 | 7.16 | 13.00 |
You might want to graph AC and MC as a function of q.
There are a number of things to notice about this chart. What the chart shows are the costs of producing various quantities of sweaters, taking into account the opportunity cost of my time. I’ve assumed that as I produce more sweaters per day, I have to pace myself and take a little bit longer per sweater to keep from making mistakes. Notice that when MC is below AC, AC falls. When MC is above AC, AC rises. Also notice that the sum of all previous MCs equals TC. What is Pe? Answer: $4.50. What is the minimum point of AC in terms of quantity, qe? There are two quantities of qe because we have assumed away fractions of a sweater. (If TC, AC, and MC, were continuous functions, that is, if we allowed for making fractions of a sweater, then the actual qe would be between 2 and 3.) If price were Pe (4.50) I would be indifferent between making 2 or 3 sweaters. In both cases, I would just break even, making zero profits. Suppose I made 2 sweaters–my revenue would be $9. I would spend $3 in raw materials ($2 for the yarn and $1 for the needles) so my income for the 2 hours of work would be $6. This would be just enough to get me to knit sweaters rather than ride the garbage truck. Actually, I would be indifferent. So, when the price of sweaters hits $4.51, I become a sweater maker but we round it to $4.50 making the assumption that when I’m indifferent I choose sweaters.
What does my supply curve look like?
Suppose the price of sweaters is $10.00. How many sweaters will I make? The answer is that I choose to make sweaters up until the point where P = MC, which in this case is 5 sweaters per day. My sweater revenue will be $50. I will have to spend $6 on yarn and needles per day, leaving me with $44 to live on. I make $44 dollars in profit—accounting profit.
However, accounting profit is not what concerns us. It doesn’t take into account the opportunities I forego to make sweaters. Instead of knitting I could be riding the garbage truck and making $3 per hour. Once we factor this opportunity cost into things, my economic profits are only $20, since I will have to spend 8 hours per day knitting that I could have spent on the garbage truck at $3 per hour (or $24). Verify that my profits will be smaller if I choose a quantity other than 5.
Now, we have taken all costs into account and at a price of $10 I will be making a $20 economic profit—I’ll be making $20 more than my next best alternative for the same amount of work.
If everybody who can drive a garbage truck for $3 per hour can also make sweaters, and can make them for the same amount I can, the price of sweaters will certainly not stay at $10. Do you see why not?
Anytime there are positive economic profits being made, those profits serve to draw other people into the activity. If I can make $20 more making sweaters than I can riding on the garbage truck and there is no reason that somebody else couldn’t make the same amount, they would be foolish not to take up knitting. In fact, as long as anyone can make more by knitting sweaters than driving a garbage truck, people would be foolish to pick up trash.
If all people have the same ability, then price of sweaters will have to fall (or the wage for garbage men will have to rise) until everyone riding on garbage trucks, and all the people knitting make zero economic profit.
Additional Questions:
- If everybody who can make sweaters can also drive a garbage truck for $3 per hour, what will the price of sweaters be? What will the supply curve of sweaters look like? (Draw a graph)
- What determines the number of people in the world making sweaters?
- What happens when there is an increase in demand?
- How will the analysis change if there is an increase in demand for garbage truck workers that drives up the wage of garbage men to $4? What will be the effect on sweater prices of this wage increase?
- How would your answer change if instead, I found a job that paid $4 and hour, but all other sweater makers still had $3 as their next best alternative?
- How would the analysis change if I figured out a way to cut the time in half that it takes to do the knitting?
- What if everybody figured it out?

