How do consumers and producers feel about equilibrium outcomes of P*, Q*? Each consumer would like to buy more, but only if the price falls. Each producer would like to produce more, but only if the price goes up. There seems to be something “good” about Q* then, but it is hard to know for sure. Maybe Q* is too large or too small. Maybe P* is too high or too low. How can we begin to know?
We would like a measure of the value consumers place on the quantities they get to consume in equilibrium when price is P*, and the value producers place on the quantities they get to produce when price is P*. If we knew how consumers and producers felt when quantity and price were something different from P* and Q* we could know something about how they feel about P* and Q*. We would also have very valuable information about how consumers and producers feel about government regulations that preclude getting to P* and Q* and tell us something about the costs of those regulations. So we now turn to evaluating how consumers feel about consuming various quantities of a good.
Let’s look at Barney’s demand for gasoline, shown below:
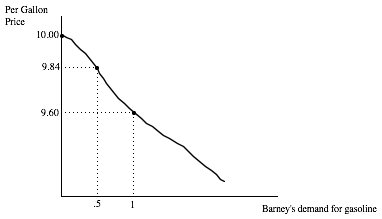
Barney’s demand curve tells us what Barney does depending on the price of gasoline. We’re going to use this demand curve to also tell us how Barney feels about various prices of gasoline.
Tell me the price of gasoline, and I can tell you how many gallons Barney will buy each week as long as nothing else about Barney changes such as his income or the prices of other goods. For example, when the price is $9.60 per gallon, Barney buys exactly one gallon per week. What is the value of Barney of this single gallon? Can we put a monetary value on it? Equivalently, how much is Barney willing to pay to have a gallon of gasoline as opposed to a situation where he does not have it? These two questions are intimately related as we will see and can both be answered by using Barney’s demand curve.
We know that when the price of gasoline is 10.00, Barney buys zero gallons. A price of $10.00 means that Barney has a choice. He can either buy a gallon of gasoline and give up 10.00 or he can pass up the gasoline and keep the 10.00 in his pocket. We see from Barney’s demand curve that when the price of gasoline is 10.00, he prefers keeping the 10.00 in his pocket to having even a single gallon of gasoline.
Try to keep in mind what is really going on in the background. The choice is not really between having a gallon of gasoline vs. having 10.00 in your pocket. There is no intrinsic pleasure produced by either of these activities. I don’t buy gasoline in order to have it, but rather to use it in my car, boat, or lawnmower for example. I buy gasoline in order to do something that gives me happiness, such as driving to the beach, fishing in my boat, or keeping my lawn neat. Similarly, I don’t pass up the gasoline in order to feel green pieces of paper inside my wallet. I’ll use them to buy something else that I value more than 10.00. So saying that Barney prefers keeping the 10.00 to the first gallon of gasoline is really saying that Barney prefers 10.00 worth of some other goods to taking a ride in the country (or whatever activity maximizes Barney’s pleasure from having a gallon of gasoline to use each week.
From the fact that Barney chooses to buy zero gasoline when the price is 10.00 tells us that Barney’s value of the first gallon is less than 10.00. But we also know that Barney’s value of the first gallon is at least 9.60. HOW DO WE KNOW THIS? When Barney was given a choice between 9.60 and a gallon of gasoline, he chooses the gallon of gasoline. So a gallon of gasoline is worth at least 9.60, else Barney would have bought less than a gallon, or zero. So a gallon of gasoline per week is worth something between 9.60 and 10.00 to Barney.
To get a more precise estimate, consider Barney’s demand for half gallons shown below:

The half-gallon demand curve has the same information as the gallon demand curve, just represented a little differently. When the price is 4.80/half-gallon, or 9.60 per gallon, Barney buys 2 half-gallons, or one full gallon. Using the same logic as before, the first half gallon is worth less than 5, but more than 4.92. How about the second half gallon. It must be worth less than 4.92, because when the price is 4.92, Barney prefers keeping the 4.92 in his pocket rather than having the second half gallon. But as before, the second half-gallon must be worth at least 4.80, because Barney buys it when the price falls to 4.80 rather than keep the 4.80. So the value of the entire first gallons is worth at least 9.72, but less than 9.92. HOW DID I MAKE THIS CALCULATION?
We can represent this improved range of value using the demand curve. The two figures below show the upper and lower bounds for Barney’s value of the first gallon:

In the first graph, the shaded area shows the underestimate. The area of the first rectangle, the checkerboard, is 4.92, (width 1/2, height 9.84), and the area of the second rectangle, the diamonds, is 4.80 (width 1/2, height 9.60). These are steps under the demand curve using the height of the demand curve at 1/2 and 1 gallon. The overestimate is shown in the second graph where the rectangles are shaded in by cross-hatching. Verify that the areas of the rectangles sum up to the overestimate of 9.92.
As you might imagine, we can improve the range of estimates by considering finer and finer divisions of a gallon. Each time we are providing a range where the lower bound is the area of a set of steps (rectangles) under the demand curve, and the upper bound is the area of a set of steps above the demand curve. As we take finer and finer divisions, the upper and lower bounds converge to an estimate of the value equal to the area under the demand curve.
The value to a consumer of a particular quantity of a good is the area under the demand curve between zero and that amount of the good. So in the figure on the left, shown below, the value to Barney of having 2 gallons of gasoline is the area under his demand curve between zero and two, or abcd. This area, which is measured in dollars, (the units on the vertical axis are dollars per gallon, the units on the horizontal are gallons, so areas are the product of the two which leaves us with dollars), is the monetary value to Barney of having two gallons of gasoline. It is the maximum amount of other goods Barney is willing to exchange for two gallons of gasoline. The value to Barney of having an additional 1.5 gallons, given that he already has a gallon, is shown in the diagram on the right–it is the area under his demand curve between one gallon and two and a half gallons, the area abcd:

For now, there are two characteristics of this value measure that are worth noting. It doesn’t make any sense to ask Barney the question: how much value do you place on gasoline. You have to add two other parts to the question. You have to tell Barney how much he already has (it may be zero) and you have to specify how much additional gasoline he is going to get.
One particular additional amount of gasoline we are interested in Barney evaluating is what you might call a “little bit more.” An easy way to define “a little bit more” is one additional unit of the good. The problem is what units are to be considered. One more unit of gasoline can be one more tanker, one more gallon, one more tenth of a gallon, one more ounce, etc. If we think about making the unit of gasoline smaller and smaller, the value of an additional unit becomes equal to the height of Barney’s demand curve. In the figure below, we see that the value to Barney of a second ounce of gasoline, given that he already has one, is between 9.99 and 9.96 per gallon. (You would have to divide these numbers by 128 to get Barney’s value of those ounces.) So if you wanted to know the value to Barney of an extra 128th of a gallon given that he already has 1/128th of a gallon already, we would say that it is between 9.99 and 9.96. The exact measure might be 9.97 or 9.98. But using the height of Barney’s demand curve at 1/128th of a gallon, 9.99 is going to be a very close approximation of the true value. Either measure is not going to be very far off:
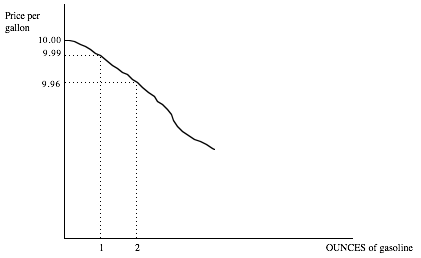
When we ask the question, what value does Barney place on having an additional GALLON (rather than an ounce) given that he starts with zero, we know the answer is something between 9.92 and 9.72. Using the height of the demand curve at either zero or one gallon is going to be close to the true measure, but not as close as when we are talking about an additional ounce. So the height of a demand curve at a particular quantity is a pretty good approximation for the value of a little bit more, as long as the little bit more is sufficiently little.
A friend of mine, when accused of drinking too much, will often reply: I only had three beers. He is usually talking about one of those special 85 oz beers. Asking me the value I place on drinking a beer will get you a very different answer depending on how you define one beer.
Some important definitions:
Marginal value (or MV) for an individual consumer is the value the consumer places on having one more unit of the good where one more unit is sufficiently small, given that he had a particular amount already. It is measured by the height of the demand curve at the particular amount specified.
Total value (or TV) for an individual, is simply the value a consumer places on having some particular extra amount of the good given that he already has some amount already. We can speak of the total value of 10 gallons given that someone has zero, or the total value of 4 gallons, given that he has fifty.
Both of these concepts carry through for the market demand curve. The figure below shows Barney, Wilma, Betty, and Fred’s demand for six packs of beer per week.
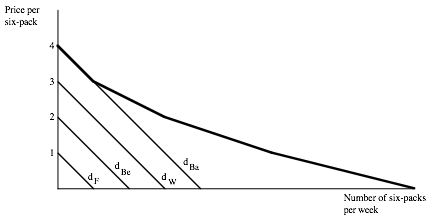
The market demand curve is shown in bold. When the price is $4 no one buys any beer. When the price of beer falls to $3 per six pack, Barney buys a single six-pack. Barney’s demand curve starts at $4 and has a slope of -1–it coincides with the market demand curve until price reaches $3 because Barney is the only customer in the market until then. When the price is $2, Barney buys two six-packs, and Wilma buys one. To keep the graph simple, I have assumed that each citizen of Bedrock shown has a demand curve for beer with a slope of -1–for every dollar increase in the price of beer, there is a one six-pack reduction in the quantity consumed and purchased.
VERIFY THAT THE MARKET DEMAND CURVE IS THE HORIZONTAL SUM OF THE INDIVIDUAL DEMAND CURVES. TAKE A FEW PRICES, SEE WHAT INDIVIDUAL DEMANDS SUM UP TO, AND SEE THAT MARKET DEMAND IS DRAWN CORRECTLY. NOTICE THAT MARKET DEMAND IS A SERIES OF KINKS, BUT NOTICE HOW SMOOTH IT LOOKS WHEN ALL FOUR PARTICIPANTS ARE IN THE MARKET.
(Suppose Ed is willing to pay $12.00 for 10 beers. When beers are $1.20 each, will Ed buy more than 10, less than ten or exactly 10 beers?)
Suppose the price of a six-pack is $1 in Bedrock. What will be the total number of six-packs purchased and consumed by our happy foursome? How will this total consumption be distributed among the four people? Consider Barney, for example. When the price is $1, Barney buys 3 six-packs per week. What is the value to Barney of three six-packs? The area under Barney’s demand curve between zero and three. Because Barney’s demand curve is a straight line, we can make an exact calculation of this area under Barney’s demand curve. It is a trapezoid-a triangle on top of a rectangle. The area of the rectangle is $1×3, or $3. The base and height of the triangle are both 3, so the area of the triangle ((bah)/2) is $4.5. So the value Barney places on having three six-packs of beer per week is $7.50.
We can make the same calculations for the three other citizens. The value to Wilma of the two six-packs she consumes is $4, the value to Betty is $1.50 for the single six-pack she consumes, and Fred consumes no beer, so the total value of his beer consumption is zero. VERIFY THESE NUMBERS. The sum of all four citizens total value for the amount they consume is $13 ($7.50+$4+$1.50+0). But notice that the area under the market demand curve between zero and 6 six-packs, the total consumed in the market, is also $13. You can prove this by adding up the triangles and rectangle under the market demand curve between 0 and 6. As you do so, you will be picking up each triangle and rectangle from the individual demand curves.
DEFINITION:
The Total Value to Society of a particular quantity of a good, is the area under the market demand curve between zero and that quantity.
Let’s see more precisely what this particular definition of value really means. We will say that the value to Bedrock of having six beers is $13. (We are assuming for simplicity that our four friends make up the entire market for beer in Bedrock.) What does it mean to say that the total value is $13? It means that if we could get 6 beers somehow, what is the maximum amount the consumers would be willing to pay to get those beers. But there is an important assumption we are making. We assume that the beers go to those citizens who value beer the most.
For example suppose we gave all six six-packs to Fred and forbade him from reselling them, under penalty of death. The total value received by the citizens of Bedrock from this gift is exactly fifty cents. Fred values the first six-pack at fifty cents (HOW DID I MAKE THIS CALCULATION?) but places a zero value on the remaining five. Suppose I wanted to maximize the value Bedrock citizens receive from six six-packs. I would give 3 to Barney, 2 to Wilma, 1 to Betty, and none to Fred. This allocation of the six six-packs maximizes the possible value from beer consumption by the citizens of Bedrock. What does it mean to say that I have maximized the possible value from the 6 six-packs? I have given the six-packs to those citizens willing to pay the most for them. So when we say that the area under the market demand curve between two quantities is the value to society of that change in beer consumption, say from 0 to 6, we are saying that is the maximum amount of money we could raise from the citizens of Bedrock for those 6 beers when we give them to the people who value beer the most.
We also mean something special by the phrase those who “value beer the most.” Who do you think likes beer the most in Bedrock? Think about it for a minute before answering. The answer seems obvious, doesn’t it? Isn’t it Barney? If you think about handing out the six available six-packs one at a time, who values the first one the most? Barney does–he’s willing to pay $3.50 for his first six-pack. Now the second one. Barney already has one. His value of a second, given that he has one already is $2.50. But this is also William’s value of her first six-pack, so in the sense of producing the most value from the gift of the six-pack, it doesn’t matter whether we give it to Barney or Wilma. Let’s give it to Wilma. Then the third six-pack being given out is valued most by Barney. With Barney having two six-packs, and Wilma having 1, who values the fourth six-pack the most? The value of the fourth six-pack is $1.50, and it is valued equally by Barney, Wilma, and Betty, so if we give six-packs 4 through 6 to each of them we will be producing the most value. We don’t have a seventh six-pack, but if we did, who values it the most? The surprising answer is that all three consumers, Barney, Betty, and Wilma, value the seventh six-pack equally, at 50¢. Each is willing to pay a maximum of 50¢ for another six-pack.
The insight here that we will come back and use shortly, is that when Barney has three six-packs, and Wilma has two, and Betty, has one, all three of them have a MV of 50¢–which is approximately equal to the height of the demand curve for each of them–$1. (Here the height of the demand curve is a mediocre measure of MV because we have defined beer broadly as a six pack. Their MV for an additional beer is about 15.2¢ which is very close to the height of the demand curve measured in beers, or 16.5¢. Be proud of yourself if you can figure this out.)
What is true in this particular case is that the TOTAL value Barney gets from his beer consumption exceeds the TOTAL value that Wilma gets from beer consumption. Does this mean that Barney gets more pleasure or happiness from his three six-packs than Wilma does from her two? What do you think? Our concept of value is not related to happiness in this way. All we know so far is that Barney is indifferent between having 4 six-packs and having $8.
So when we say that the area under the demand curve is the most we could collect by giving the good to the consumers who value it the most, we don’t mean necessarily that we give the good to the consumer with the highest demand curve or even with the most area under it. It means we give the good out unit by unit to the people willing to pay the most for each one.
We can define the marginal value of beer for the town of Bedrock just as we defined it for an individual. The marginal value of beer in Bedrock when Bedrock has six beers already, is the amount we could collect from SOMEONE in Bedrock if we had a little bit more beer. What is the value to Bedrock of an additional 1/10th of a six-pack–7.2 ounces of beer. If we had an extra 7.2 ounces of beer we could sell it to the citizen who values it the most. In this case the citizen willing to pay the most for it is any of three citizens, Barney, Wilma, or Betty. Since each is willing to pay about $1.00 per six-pack for an extra bit of beer, they would each pay about 10¢ for an extra 7.2 ounces. So the value to Bedrock from having an extra 7.2 ounces is 10¢.
To review: the demand curve tells us the quantity demanded at various prices of a particular good. Demand curves capture what people would like to do at various prices. Demand curves capture the willingness of market participants to purchase the good. Not surprisingly, the decision to purchase a good has embedded in it an implicit statement about value. We have shown that the value of additional amounts of the good can be measured by the area under the demand curve.
Not surprisingly, the supply curve of a firm–the relationship between price and the willingness of a firm to supply a good, has embedded in it what it costs the firm to supply the good. A firm will only be willing to supply amounts of the good at a particular price if it is able to cover its costs of production, inclusive of opportunity costs. We will use the following results without proof:
The total cost of x units of production for a particular firm, is the area under that firm’s supply curve between zero and x. Marginal cost is the cost of producing one more unit of the good, given a particular level of production already. Marginal cost is approximated by the height of the supply curve as long as the definition of an extra unit is sufficiently small. The total cost to society of x units of production is the area under the market supply curve between zero and x.
Our concept of cost includes opportunity cost, what the owners of the firms give up to produce the good being discussed. In the case of apples, the cost includes the direct payments the farmer makes to buy fertilizer and seed and machinery to plant and harvest, but it also includes what the farmer could have done with these resources (including the land) if he did not use it to grow apples.
The true cost to our little society of Bedrock of growing and selling 28 apples is the area under the market supply curve between zero and 28. There are two equally correct ways to think about this cost. One is essentially arithmetic–add up the costs of each firm in the market making sure to include a measure of opportunity cost for the resources used. (I’ll make this clearer in a minute). The second measure is more conceptual–the cost of 28 apples are the other things Bedrock can’t have because it has devoted time and energy and resources to growing apples.
Efficiency–A Central Application of the Concepts of Cost and Value
Suppose you are the King of Bedrock. You can decide whether Bedrock will have farmers growing apples. If it does, you will decide how many apples Bedrock will grow and harvest. You will decide who will eat the apples and how many will go to each citizen. A moment’s reflection reveals the difficulty of the problem. Even if you as King could read the minds of your subjects and knew exactly what would make them happy, you have to have a rule about how to weigh the happiness of one citizen against that of another. But you cannot even read the minds of your citizens. All you know is the supply and demand curve for apples shown in figure .
Apple suppliers come to you desiring that you decree massive apple production to be sold at very high prices. Apple demanders come to you asking for massive apple production but for apples to be free. Some citizens do not even like apples, and they ask that apple production be zero.
After weeks of frustration having all your citizens troop before you in search of special treatment, you despair and decide that for the moment, you are going to let citizens buy and sell apples freely, and see how things turn out. You observe that the price of apples is $1.50, and that 28 apples are sold per week.
Is this good or bad? Let’s see if we can improve things somehow. First are the 28 apples that are being produced being produced by the farms at the least cost. Perhaps one apple firm should expand its production, another contract its production resulting in a gain of resources. This is considered below in figure 200:

The figure focuses on two firms, A and B. At the price of $1.50, B is producing q*B while A is producing a smaller amount, q*A. If A cut back production by one unit, the saving would be the area under A’s supply curve, sA, between q*A-1 and q*A. This is shown in the figure as a checkerboard. If B expanded production, the extra costs would be the area under B’s supply curve. sB, between q*B and q*B+1. This is shaded in with diamonds. Which area is larger–the diamond shaped area. Both areas have width of one unit, but the extra cost to B is greater than the savings from A.
Given that each firm faces the same price of $1.50, each one has chosen the point on its supply curve where the height of the supply curve is equal to price. The height of the supply curve is marginal cost, the cost of producing a little bit more. So every firm has the same cost of producing a little bit more. But the cost of producing a little bit more is always greater than the cost of producing the previous unit. (Is this a fact or an assumption? How is it represented graphically?) As a result, as long as all firms have chosen levels of output such that their marginal costs at their respective outputs are identical, any rearrangement of output within firms can only increase costs.
In a competitive market, there is no way to rearrange production and thereby lower the cost of production. The allocation of output within firms cannot be improved on.
How did this happen? Given the price, each firm is producing an amount that maximizes its profits. Look at firm B’s supply curve in figure 200. If it expands output to q*B+1 when the price is $1.50, it gains extra revenue of $1.50, but incurs costs of more than $1.50. (Prove this last statement.) The self-interest of every producer insures that all firms have the same marginal cost. This insures that the right firms produce Q*.
What is happening on the demand side? On the demand side, each consumer expands consumption until the value of the last unit is just more than the price, but the value of the next unit is just less than the price. If this were not true, then the consumer can be happier choosing a different quantity of the good. So each consumer who is consuming a positive amount of the good (as opposed to zero) values another unit at slightly less than the price, but is willing to give up a unit of the good for slightly more than the price. Can one consumer sell one of the apples he has purchased to another consumer and be better off? Yes, as long as he gets more than $1.50 for it. Is there a consumer willing to pay even $1.50 for one more apple? No. Every consumer is willing to pay less than $1.50 for one more apple. If they were willing to pay $1.50 or more, they would have bought one in the market place.
Can a rearrangement of apple consumption among consumers make anyone better off? Sure. Take an apple from Barney and give it to Wilma. Wilma will be better off. But Barney is worse off. Given the price of $1.50, and the 28 apples that are available, there is no way to rearrange them in such a way as to make anyone better off unless we are willing to make someone worse off. We know this from the analysis in the paragraph above–if a taking one apple from one consumer and giving it to another could make them BOTH better off, then they could have arranged a deal. The fact that they cannot tells you that one person can only be better off at the expense of another.
The market price of apples of $1.50, where consumers are free to purchase as many apples as they want at that price results in maximizing the value from the 28 apples. The apples go to the consumers who value them the most. There are no exchanges possible among consumers that can make someone better off without making someone worse off. These are all saying the same thing. We express it formally by saying that the distribution of apples among consumers is Pareto efficient. A Pareto efficient distribution means that no one can be made better off without making someone worse off. This sounds negative, but it really is a minimally attractive characteristic about the distribution of apples. If someone could be made better off without making someone worse off, we should go ahead and make the person better off. To say that the distribution is Pareto efficient is to say that all of these possible improvements in people’s happiness have already taken place. And that is good.
What about the total number of apples? Is 28 too high or too low? A 29th apple seems good, lots of people would like one more apple rather than not having one. A 29th apple has a cost however. The cost in one sense is the cost of producing that apple–the time, effort, and resources, necessary to produce one more apple. But the true cost to society is the value of the goods we could have produced with that foregone time, effort, and resources. We know how much this cost is. It is the area under the market supply curve between 28 and 29 apples. We also know the value to society of having the 29th apple instead of those other things we could have produced with the time, effort, and resources. The value of the 29th apple is the area under the demand curve between 28 and 29 apples.
Which is greater, the cost or the value of the 29th apple? The cost. The 29th apple is not worth producing. The cost to society of the 29th apple exceeds the benefit to society. What do we mean by society? Is society an independent entity with tastes and feelings of its own. Not here. When we say the cost to society is the area under the supply curve, we mean that someone in society is going to lose the area under the supply curve between 28 and 29. We can think of the firm as having to pay this cost, but you can also think about the person who would have received the value of the alternative use of the resources going to the 29th apples. When we say the benefit to society of the 29th apple is the area under the demand curve, we mean that someone in society is willing to pay the area under the market demand curve between 28 and 29. We can identify this person–it is the person with the highest value of the 29th apple. The gain to this person is less than the cost of producing the apple. So it is wasteful to produce the 29th apple.
Another way to see this waste is to think of Pareto efficiency. Can we increase the production of apples and make someone in society better off without making someone worse off? The answer is no. The quantity of apples is Pareto efficient. This is another way of saying that given that there are 28 apples being produced and eaten, no consumer is willing to pay enough for one more apple to make it worth the while of a producer to go ahead and produce it. This is rather remarkable. You should be able to convince yourself that it is also wasteful to contract production by one apple to 27.
In the unconstrained free-market solution of P* and Q*, the following holds:
1. Apples are produced by the firms at the least possible total cost.
2. Apples are eaten by the consumers who value them the most.
3. The total quantity of apples is efficient–devoting more or fewer resources to apples produces waste.
The market is extraordinary. By letting buyers and sellers exchange goods freely, a market price and quantity are established that takes advantage of all the possible exchanges between seller and seller, buyer and buyer, and buyer and seller that could possible make any two parties better off from the exchange.
Sounds great, huh? Let me play the critic: “The free-market looks good alright, but the whole analysis relies on the concept of value. The definition of value is willingness-to-pay. This is ridiculous. Suppose Charlie is a millionaire and Buster a pauper. Suppose there is only one apple available. Who should get it? In the free-market solution, Charlie gets it, because he is willing to pay more. He outbids Buster for it. What’s efficient about that? How can you say Charlie values the apple more than Buster. Maybe Buster really values it more than Charlie, but because he’s poor, he can’t pay enough to outbid Charlie. I say that because Buster’s poor, he should get the apple. Forget Charlie. He’s just a rich pig who has plenty of other toys anyway. To conclude that the free-market solution is efficient because it maximizes value is just to play with words like value to suit your own meaning. True value is psychological and has nothing to do with willingness to pay.”
This sounds pretty good, too. Is it right? Not really. It’s right in the sense that our definition of value uses willingness-to-pay. This is not the only way to define value, but we will see that it is a useful way. For now let’s see if Buster, who is allegedly being victimized, thinks it’s a useful way.
Suppose Buster consumes zero apples when the price is $1.50. They’re too expensive. The other consumers have outbid him for the 28 apples available. Worse, he can’t offer enough to any of the producers to induce them to produce a 29th apple for him. Buster may not be poor. He may not be consuming any apples because he doesn’t like them that much. But to make the strongest case against the free-market solution, let’s assume Buster is poor, and that is why he isn’t willing to pay much for apples. Apples are his favorite fruit–he just doesn’t have much money and his willingness to pay for apples is low, compared to his willingness to pay for clothes, food, and other items that he prefers to apples.
Suppose you reject our concept of willingness to pay as a useful measure of value. You think Buster should have an apple, even though he chooses not to buy one. There are two places to get apples. We can give Buster one of the 28 apples already going to someone else. Or we can get a firm to produce another apple. Let’s examine each of these solutions. First, let’s take away one of Charlie’s apples and give it to Buster. Does this make Buster better off? Sure. Buster enjoys the apple. Charlie is less happy. But since Charlie is a millionaire, and Buster is a pauper, you might feel it is justified to redistribute apples in this way. (We are ruling out the possibility that Charlie gives Buster an apple voluntarily.)
Buster has an apple. Will he eat it? Maybe not. He might instead sell it to Charlie. We know approximately how much Charlie is willing to pay for the apple he has lost. His lost apple is worth a little more than $1.50, since we know he purchased it for $1.50 before. He would pay at least $1.50 to have it back. Is Buster willing to sell it for $1.50? Sure. His previous decision to buy zero apples tells you that he prefers $1.50 to a single apple. Suppose Buster’s willingness to pay for one apple is $1.00. Then how much would he have to receive from the sale of the apple to make the sale worthwhile? At least $1.00. He prefers $1.01 of other goods to one apple.
Buster is willing to sell the apple if he gets at least $1.00. Charlie is willing to buy the apple as long as the price is less than $1.50. If Buster sells the apple to Charlie for a price between $1.00 and $1.50, both Buster and Charlie will be better off than if the sale did not take place.
Suppose the sale does take place at a price of $1.35. The apple will end up in Charlie’s stomach just as it did before. The free-market solution occurs just as it did before, in the sense that the people who “value” the good the most are the ones that get it. There is a difference, though. Buster gets an extra $1.35 of goods other than apples, while Charlie has $1.35 less. Still upset? Do you believe that Buster still values the apple more than Charlie and should be the one to consume it? We could prohibit Buster from reselling the apple. Both he and Charlie will try to get around this prohibition, so we will have to devote resources to stopping the sale. This may mean using people who used to produce apples to be policemen, and so we will have fewer apples than before. But maybe Buster will have trouble finding Charlie, and will give up and choose to eat the apple himself. Buster will get the same satisfaction he gets from the apple that he would have gotten from $1.00’s worth of other goods. But if we had let Buster sell the apple, he would have gotten the satisfaction from $1.35 worth of goods. Not letting Buster resell the apple is wasteful. It hurts Buster. (It also hurts Charlie. By how much?)
Giving Buster one of Charlie’s apples and making him eat it makes society worse off. There is a net loss to its individual members. In this case, both Buster and Charlie are worse off if we prohibit the resale of the apple. Below we will consider a way to help Buster without giving him an apple. For now, we have seen how the market solution insures that the people who value the good the most are the ones that consumer, and how, in a sense, this honors the choices of both Charlie and Buster.
OK. So maybe it is in Buster’s interest not to consume apples when there are only 28. But what about getting a producer to grow one more apple and give it to Barney? The cost of producing the extra apple is at least $1.50. We know this because all producers have marginal cost of $1.50 in equilibrium. Giving an apple to Buster gives him the same pleasure he gets from $1.00 worth of goods other than apples. The fact that the marginal cost of producing the next apple is at least $1.50, says that the resources used to produce the last apple, could instead go to produce at least $1.50 worth of other goods. Giving Buster the apple instead of those other goods makes Buster worse off, by at least 50¢. He would prefer the other goods to the apple, or the money necessary to buy them.
We argued above that pushing apple production past Q* is wasteful–the value of the extra production (the area under the demand curve), is less than the cost (the area under the supply curve). To increase production past Q* is wasteful. The waste is not that people who don’t buy apples or who buy a small number should be ignored and it is wasteful to try to help them. The waste is that these people on the demand curve to the right of Q* prefer the money used to produce apples to the apples themselves. Going past Q* is the wrong way to go about helping poor people who like apples but choose not to buy any. Our measure of value captures this effect.
The Role of Prices
The net gain to society from having Q* apples (as opposed to not having any) is represented in the diagram below:

In the diagram on the left, the net gain to society is shown as the triangular cross-hatched area. It the difference between the area under the demand curve minus the area under the supply curve from zero to Q*. This is usually the easiest way to calculate gains to society.
The diagram on the right shows the same area but calculated differently. Consumer surplus is the net gain to consumers. The consumer surplus for a particular amount of a good is the area under the demand curve between 0 and the amount of the good, minus the monetary cost of acquiring that amount of the good. In the diagram on the right, the consumer surplus of Q* apples is the area under the demand curve between 0 and Q*, minus the amount consumers have to pay for Q* apples. This amount, P*xQ* is represented in the diagram on the right by a rectangle whose height is P* and whose width is Q*. So consumer surplus is the shaded triangular area with the VERTICAL lines.
Producer surplus is the net gain to producers, the difference between revenue and costs. This is also defined as profit. Producers receive revenue of P*xQ*. Their cost is the area under the supply curve. Producer surplus, or profit, is shown in the diagram on the right as the shaded triangular area with the HORIZONTAL lines.
(You can talk about consumer surplus for a single consumer, or a group of consumers as we have done here. For example, if you value seeing the Red Sox on Opening Day at $35 and the ticket costs you $5, you receive consumer surplus of $30. Similarly, you can talk about a single firm’s profit or producer surplus.)
The diagram on the right decomposes the total net gain to society among the groups that receive that gain, consumers and producers. There are two ways to figure out the total gain to society. The first is shown in the diagram on the left–look at the total quantity consumed. Take the area under the demand curve up to this quantity consumed. These are the benefits to society. Then look at the quantity produced–in this case, as it is in any case where the market is unconstrained, the quantity produced is the same as the quantity consumed. Take the area under the supply curve between 0 and the quantity produced. These are the costs to society. Subtract the costs from the benefits and you get the net gain to society. The alternative method is to take the net gain to each group and add up these net gains.
Prices play a number of roles in a market. Prices are a signal to producers about the return to producing another unit. Prices are a signal to consumers about the cost of consuming another unit. It is this signaling role of prices that insures that Q* units get produced. This is the allocative role of prices. Prices also play a distributive role in determining how the net gain to society of the Q* units is divided among producers and consumers.
But we could think of alternative ways of producing Q* units. Suppose we forced producers at gunpoint to produce Q* units and gave away these units to consumers. Using the method on the left, the gain would again be the area under the demand curve (the benefit to society) minus the area under the supply curve (the cost to society.) In this case the net gain would again be the cross-hatched area. (How do consumers and producers divide up this gain? What allocative role of prices that occurs in the market solution have I implicitly assumed would also be achieved by the gunpoint solution?) Similarly, we could tell producers to produce Q* apples and at gunpoint, make consumers pay $1000 per apple. The net gain is again the cross-hatched area.
Consider the three methods of achieving Q*–the market, enslaving producers and exploiting consumers. In each case, the net gain to society is the cross-hatched area. PRICE PLAYS A CRUCIAL ROLE IN DETERMINING QUANTITY IN THE MARKET SOLUTION, BUT ONCE QUANTITY IS DETERMINED, YOU IGNORE PRICE IN CALCULATING THE NET GAIN. IT DOESN’T MATTER WHETHER CONSUMERS GET THE APPLES FOR FREE, OR WHETHER THEY PAY $1000, OR WHETHER THEY PAY P*. THE NET GAIN IS ALWAYS THE CROSS-HATCHED AREA. ONCE QUANTITY IS DETERMINED, PRICE ONLY PLAYS IN ROLE IN DIVIDING UP THE NET GAIN BETWEEN CONSUMERS AND PRODUCERS.
In the market solution, the net gain is the cross-hatched area. But what about the revenue producers receive. Haven’t we ignored it by just looking at the areas under supply and demand curves? We have ignored it but it was right to do so. It is true that suppliers gain P*xQ* in the market solution. But this is exactly canceled out by the loss to consumers of P*xQ*. The revenue received by producers, paid by consumers is a TRANSFER of resources, and is thus neither a benefit nor a cost. In general, monetary payments from one group to another are transfers to be ignored in calculating the net gain to society. The advantage to using the method of calculating net gain that focuses on quantities is that it makes sure that transfers get ignored, as they should be.
It is convenient to ignore prices when determining the net gain to society. But it is a bit of sleight of hand to say that the three ways of achieving Q*, the market, enslaving producers, and exploiting consumers at a price of $1000 really all produce the same net gain of the cross-hatched area. In fact, it would be impossible to produce the gain of the cross-hatched area without using the market solution. Otherwise how would you know to produce Q*? How would you know which producers to put to work at gunpoint? How would you know which consumers to give the apples to? (Think about how the net gains would change given these problems.)
SUMMARY
In the previous pages we have seen how equilibrium is determined in an unconstrained market. The market clears at price P* with Q* being consumed and produced. There is no way to reallocate the Q* units consumed among consumers and make someone better off without making someone worse off. There is no way to reallocate the Q* units produced among producers to make some producer better off without making some producer worse off. The total amount of production is also efficient–increasing or decreasing production or consumption from Q* involves a loss to society. To see this vividly, consider an increase or a decrease in the quantity consumed and produced. Does the net gain exceed the cross-hatched area. It must be smaller. (Notice that by using the benefit-cost method in the left-hand diagram, we don’t have to specify what causes the increase or decrease in quantity.)
When markets are constrained by government regulations, the market may no longer clear at P*, Q*. When considering any government regulation, you should always figure out its effect on the equilibrium, and then figure out the effect on the net gain to society. We will call any decrease in the net gain to society, waste, a dead-weight loss, or inefficiency. These terms will be used interchangeably.
For example, suppose for some reason, society instead of consuming and producing Q*, consumed and produced Q1 to the right of Q*. The market would never go to Q1 on its own, but for many reasons that we shall see below, consumers and producers might be induced to go to Q1.

The value of the consumption between Q* and Q1 is the area under the demand curve. The cost of producing those units is the area under the supply curve. The cost exceeds the value by the shaded area. We value the extra production but not as much as we value the alternative things we could have produced. This is a net loss to society–we call such a net loss a waste. What is remarkable about the tools of cost and value that we use from the areas under the supply and demand curves is that it doesn’t matter what prices are paid for the good. To see this, let’s take a simple example.
Fred wants to buy a pair of gloves. He sends his friend Barney to the flea market to get him a pair. He gives Barney these instructions: “There’s a guy at the flea market who knits gloves. They’re really nice. I don’t know how much they cost, but I’m willing to pay up to $10. If they’re more than $10, don’t buy them. (What is the value Fred places on having a pair of gloves?) Try to negotiate and pay as little as possible.” Meanwhile, Gil Glover is setting up his stand at the flea market for the day. Gil sells gloves part time. He has another job that pays $4 an hour that he can work at if he wants. It takes Gil an hour to knit a pair of gloves. The yarn and needles cost Gil a $1 for a pair of gloves. Assume that the relative pleasantness of his other job and the thrill he gets from standing around at the flea market just cancel out. So what is the minimum price Gil is willing to accept to sell a pair of gloves? Five dollars. If he finds that no one is willing to pay more than $5 for a pair of gloves, he will stop knitting and showing up at the flea market.
Barney shows up at Gil’s stand. What can we guess will occur? First, Barney will buy a pair of gloves, and Gil will sell a pair. Second, the price they agree on will be between $5 and $10. Suppose they agree on a price of $7. Fred has a net gain of $3, ($10-$7) and Gil has a net gain of $2 ($7-$5). The net gain to the combined society of Fred and Gil is $5. Now suppose Barney is dishonest, diverts Gil’s attention and steals a pair of gloves while Gil isn’t looking. Net gain to Fred: $10 (assuming no guilty conscience). Net gain to Gil: -$5. Net gain to the twosome is again $5. Suppose Barney misunderstood Fred and pays $20 for the gloves. Net gain to Fred: -$10. Net gain to Gil: $15. Net gain to the twosome: $5.
The price paid between Fred and Gil is a transfer. The net value of the transaction is always the area under the demand curve minus the area under the supply curve: Fred’s value minus Gil’s cost (inclusive of opportunity cost) or $5. The price determines who gets to capture the pleasure Fred gets from wearing the gloves. When the gloves are stolen, Fred gets all the pleasure and Gil bears all of the cost. When the price is between $5 and $10, the two men share the pleasure and the cost.
Consider another way Barney can mess up. Suppose Barney misunderstands Fred and buys two pair of gloves. Suppose Fred value a second pair, but only at $3–he likes a second pair because then he can launder one pair and still wear the others. For this convenience he is willing to pay $3. Barney and Gil negotiate and agree on a price of $7 as before. But now Barney buys two pairs of gloves at the price of $7. What is the net gain to our two person society of Gil and Fred from the transaction on the second pair of gloves? Their value is $3. Their cost is $5. The net gain is -$2. It is wasteful for the combined twosome to exchange a second pair of gloves. Either one of them may be better off from the transaction. When Barney pays $7 for the second pair, who is better off and who is worse off? What is the net effect? The combined effect must be negative and negative by $2. The area under the demand curve is less than the area under to the supply curve just as in the case of going to Q1–there is waste. (If Barney had paid $6 for two pairs would Fred say its OK because he still has a net value of $1? See how the money paid is irrelevant for calculating the net gain or loss?)
Fred, acting on his own, would never buy a second pair of gloves. If a policeman put a gun to his head and said you must purchase a second pair at $7, the net effect would be a $2 loss compared to the situation where they stopped at having bought and sold a single pair. If a policeman put a gun to Gil’s head and said you must give Fred a second pair for free, the net loss is $2.
The cost of a second pair is greater than the value. If the policeman held the gun to Gil’s head to help Fred get a free pair of gloves, he’s using a wasteful way of helping Fred. Ultimately he is spending $5 to produce $3 worth of value. What the policeman should do is tax Gil $5. Gil will work an extra hour at his part-time job and give the money to Fred. Gil is indifferent between working the extra hour at the part-time job and knitting the gloves. But Fred gets $5 worth of pleasure now instead of $3. Society gains $2 compared to the world of forcing Gil to knit a pair of gloves and give them to Fred. Going past Q* is wasteful–going past the point where individuals would voluntarily go on their own. Fred isn’t willing to offer Gil a price for the second pair that makes it worth Gil’s while to knit them. To force him to do so is wasteful.
There is also waste if something stops Gil and Fred from buying and selling the first pair of gloves. Suppose Barney gets drunk and falls down an open manhole. By the time he gets out, the flea market is closed. Fred returns to Barney and says, I didn’t buy you anything. Gil doesn’t meet Barney. He goes home without any orders. Is there a loss? You might be tempted to say that nothing is lost. Fred still has his money, and Gil still has his time and yarn. In one sense, Fred hasn’t lost anything–he breaks even on the day–he doesn’t get any gloves but he doesn’t spend any money either. Similarly, Gil has broken even.
But this is wrong. Society is poorer. Fred’s hands are cold. (You night argue he can wear socks on his hands, but we know that this doesn’t work as well for Fred, or isn’t as fashionable, and figure out the difference between Fred’s value from gloves versus socks.) the coldness of Fred’s hands if Barney falls down the manhole is a loss of $10. But that isn’t the loss from Fred not getting the gloves. If Barney falls down the manhole, Gil has a spare hour and the yarn goes to help make a sweater and the needles become part of a car door. But you should be able to see that there is a waste of $5–foregone value above and beyond the cost that is forfeited because the transaction does not take place. Suppose if you put this down and went out for a beer you would meet the marital partner of your dreams and live happily ever after. But instead you keep reading. Wouldn’t it be wrong to say that if you keep reading you haven’t lost anything?
When quantity for some reason is stopped short of Q*, we can show the loss of foregone value greater than cost in a diagram:

If for some reason, the market stopped short of Q*, at Q0, there would be waste of the shaded area. The value of the transactions between Q0and Q* exceeds the cost. To not enjoy that value is wasteful–society gives up the net gain of the shaded area on those transactions–a waste–foregone value greater than cost that could have been enjoyed. Who would have enjoyed that net gain of the shaded area if consumption and production expanded to Q*? We don’t know. Presumably it would have been shared by consumers and producers. The sharing would depend on the price. But you should see from the story of Fred and Gil that no matter what the price, the net gain would be the shaded area.

